Hello,

Les auteurs de Malware écrivent le code de leur payload avec 3 préoccupations techniques principales:

1. Atteindre l’objectif malicieux (Chiffrer, Voler, Evader, Détruire, Usurper) : c’est la raison d’être de leur Payload
2. Passer sous les radars des logiciels de sécurité (ex: EDR, AV) en étant le plus discret et surtout atypique possible
3. Rendre la tache des Malware Analysts la plus complexe possible (Anti-Debug tricks, cryptage, offuscation, …)

C’est pourquoi les malwares font une utilisation intensive de différents algo de chiffrement symétriques et asymétriques. Il est donc nécessaire d’en maîtriser quelques-uns pour pouvoir identifier et comprendre “le petit manège”.

Je vous propose de commencer par le plus simple de ces algo de chiffrement : RC4

Son histoire

RC4 (Rivest Cipher 4) est un algorithme de chiffrement en continu conçu en 1987 par Ronald Rivest (l’un des inventeurs du RSA). Les détails de RC4 furent initialement tenus secrets mais en 1994, une description du chiffrement fut postée de manière anonyme sur la liste de diffusion USENET alt.cypherpunks.

RC4 a été utilisé dans des protocoles comme WEP, WPA et TLS.

Les raisons de son succès sont liées à sa grande simplicité et à sa vitesse de chiffrement. En revanche, son utilisation dans le cadre de protocole de sécurité est terminée en raison de certaines faiblesses mise à jour. En effet RC4 n’utilise pas de vecteur d’initialisation, en plus de la clé. Un vecteur d’initialisation indépendant de la clé permet de garantir une sécurité suffisante. Ainsi les même messages chiffrés deux fois avec la même clé ne produisent pas la même sortie. Malgré ses faiblesses, RC4 est encore massivement utilisé par les malwares.

RC4 est un algorithme de chiffrement en continu, également appelé chiffrement à flot (stream cipher). Le chiffrement à flot est l’une des deux grandes catégories de chiffrements modernes en cryptographie symétrique; l’autre étant le chiffrement par bloc. Un chiffrement à flot est constitué d’un générateur de nombres pseudo-aléatoires avec lequel on opère un XOR entre un bit à la sortie du générateur et un bit provenant du message à chiffrer.

Aux cotés de RC4, l’on trouve d’autres (plus modernes et plus sécurisés) algo de chiffrement à flot : notamment SALSA 20, dont on remarque l’utilisation croissante dans les malwares.

Principe du chiffrement RC4

La clé RC4 permet d’initialiser un tableau de 256 octets en répétant la clef autant de fois que nécessaire pour remplir le tableau. Par la suite, des opérations très simples sont effectuées : les octets sont déplacés dans le tableau, des additions sont effectuées, etc. Le but est de mélanger autant que possible le tableau. On obtient alors une suite de bits pseudo-aléatoires qui sont utilisés pour chiffrer les données via un XOR.

Pour générer le flot de bits, l’algorithme dispose d’un état interne composé de 2 parties :

1. Une permutation P de tous les 256 octets possibles
2. Deux pointeurs i et j qui servent d’index dans un tableau

La permutation est initialisée grâce à la clé de taille variable et au key schedule.

Nous avons donc une séquence de chiffrement/déchiffrement très simple, composée des 4 étapes séquentielles suivantes :

1. Initialisation de notre tableau d’état interne
2. KSA du tableau d’état avec notre clé
3. Generation du Keystream avec un PRNG
4. Exécution du XOR “membre a membre” entre l input et le Keystream

Chacune de ces étapes sont simples et trés identifiables (nous allons y revenir …)

La pratique en C

Vous trouverez ci-dessous mon implémentation de RC4 en C. Celle-ci n’est pas optimisée et vous en trouverez certainement des meilleures sur le net. Par exemple, je laisse le soin au compilateur C de trouver la meilleure optimisation de mes opérations de modulo (nous allons vite disséquer/vérifier cela en ASM reversé…) Néanmoins j’estime qu’implémenter soi-meme un RC4 est un exercice intéressant.

Toutes les explications sont dans les commentaires.

Identifier l’usage de RC4 dans un code binaire

Maintenant que nous connaissons un peu mieux RC4, on peut en tirer les macro-facteurs d’identification suivants (tous reliés par un AND ;-) :

• Commence par une boucle d’init de 256 (100h)
• Réalise des Modulo 256 (100h)
• Une boucle KSA de 100h itérations
• Procède à des swaps
• Utilise une clé unique

Compilons notre implémentation exemple, puis posons la sous notre microscope IDA afin de pointer chacune des étapes. Comme nous sommes en mode tuto, j’ai été sympa et j’ai compilé le programme C en incluant les informations de debug dans le binaire ;-) , évidemment dans le malware cela ne sera jamais le cas (sauf pour les plus mauvais d’entres-eux).

Mais avant d’ouvrir IDA, il nous faut faire un focus sur la fonction MODULO.

Reconnaitre un modulo en assembleur

Nous savons que RC4 réalise des opérations de Modulo 256.

Il existe plusieurs manières d’implémenter un mod 256 en ASM:

1. Une très/trés lente pour nos processeurs i64, basée sur des DIV ou IDIV ici pour creuser le sujet
2. Une optimisée, reposant sur des multiplications et des décalages de bit

The good Way

256 étant un nombre pair (c-á-d dont la division euclidienne par 2 donne un reste à 0), alors nous allons pouvoir calculer notre modulo par décalage de bit. Rappelons d’abord les grands principes du décalage de bit:

• Décaler de N bits vers la droite (») revient à diviser par 2 puissance N
• Décaler de N bits vers la gauche («) correspond à une multiplication par 2 puissance N

short a = 0b00011100; // soit 28 en décimal
short b;
b = a << 2;
// b vaut maintenant 0b01110000 // 112 en decimal, soit 28 * 2^2  
b = a >> 4;
// b vaut maintenant 0b00000001 // 1 en decimal (pour la partie entière), soit 28 / 2^4
a <<= 3;
// a vaut maintenant 0b11100000 // 224 en decimal, soit 28 * 2^3

Par conséquent, le compilateur (ex: x86-64 gcc -O2) implémentera notre mod 256 de la manière suivante :

        mov     edx, edi
        sar     edx, 31
        shr     edx, 24
        lea     eax, [rdi+rdx]
        movzx   eax, al
        sub     eax, edx
        ret

ou encore avec x64 msvc:

a$ = 8
int modulus(int) PROC                             ; modulus
        mov     DWORD PTR [rsp+8], ecx
        mov     eax, DWORD PTR a$[rsp]
        cdq
        and     edx, 255                      ; 000000ffH
        add     eax, edx
        and     eax, 255                      ; 000000ffH
        sub     eax, edx
        ret     0
int modulus(int) ENDP                             ; modulus

Notre boucle de 256 itérations d’initialisation se présente sous la forme suivante:

initialize(char*):
        xor     eax, eax
.L2:
        mov     BYTE PTR [rdi+rax], al
        add     rax, 1
        cmp     rax, 256
        jne     .L2
        ret

Une fois l’utilisation de RC4 identifiée par ces différents signaux, il faut alors vous mettre en recherche de la génération KSA afin d’y localiser et extraire la clé magique ;-) Attention néanmoins les auteurs de Malware utilisant RC4 aiment bien flouter un peu leur clé, mais là encore le reverse du code nous permet d’inverser celà.

1. Tiens tiens, une boucle d’init de 256 itérations …

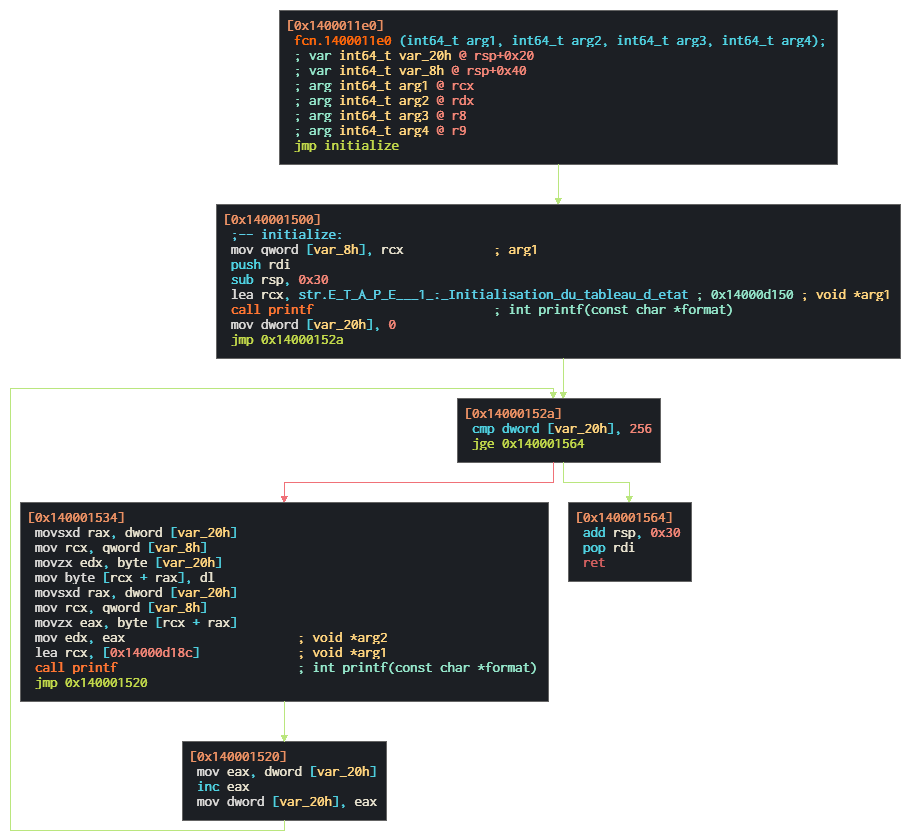
2. Boucle de XOR avec le Keystream

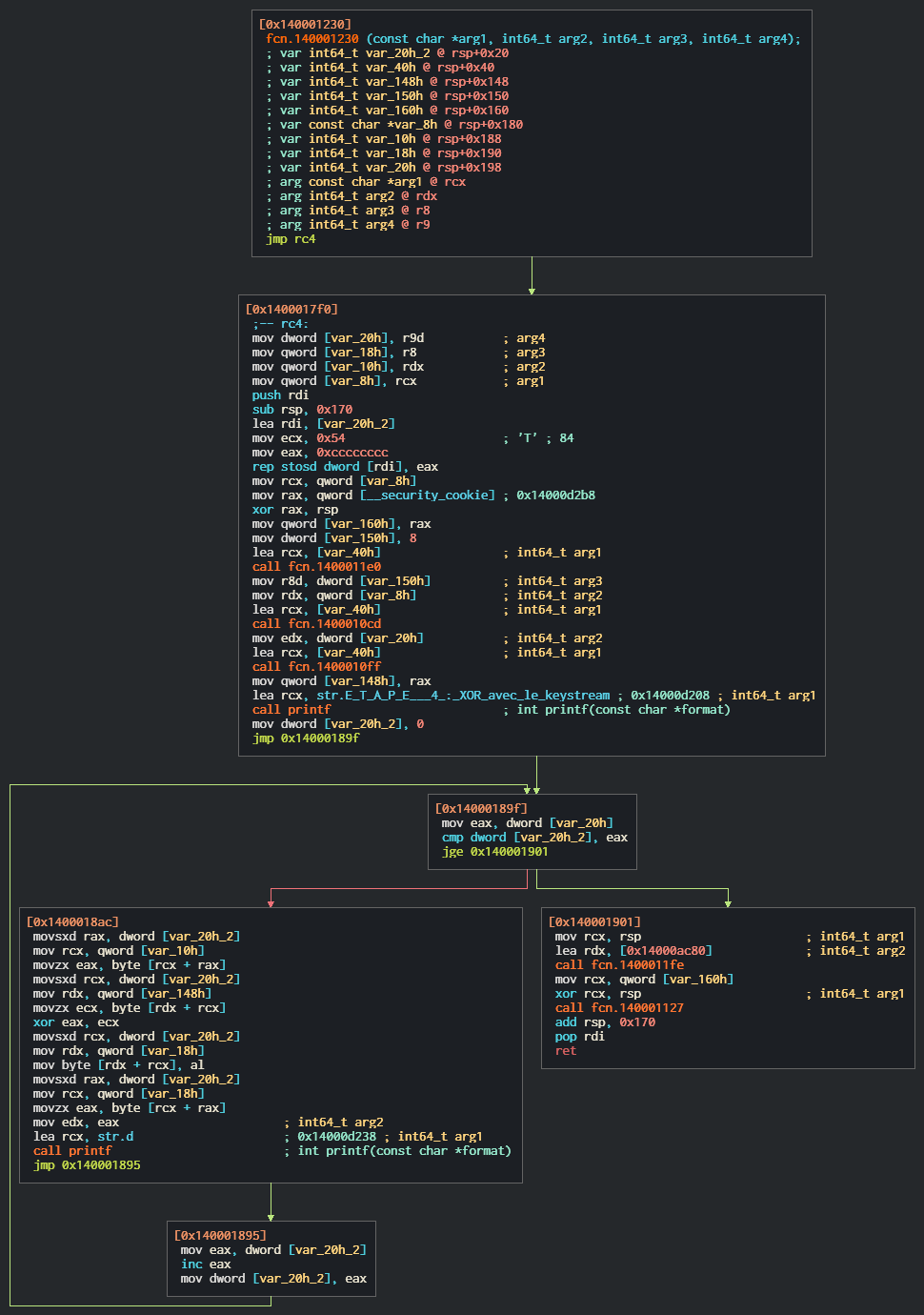
Commencer à dissimuler : les String du binaire

Evidement un malware ne stockera pas sa clé secrète en clair dans une simple string; comme c’est ici le cas dans notre programme exemple (u_char *key = "password"). Un simple examen des String dans les sections Data du binaire permettrait alors d’afficher les string candidates à être une clé déchiffrement (surtout quand la clé est “password” ;-)

L’auteur d’un malware masquera donc ses String avec des procédés tel que celui qui consiste à ajouter/soustraire/modulo inverse/… un chiffre aux octets de sa chaine de caractère, puis à les Pusher sur la pile. Ainsi une simple recherche des String dans les premières phases de l’analyse statique ne donnerait aucun indice ASCII.

Disons pour notre exemple que nous souhaitons dissimuler password en additionnant 3 aux octets de la chaîne puis les pousser sur la stack. (Si vous cherchez CyberChef, il est par là ;-)

• password = 0x64 72 6f 77 73 73 61 70 (je rappelle que nous sommes en Little Endian sur nos processeurs)
• on ajoute 3 = 0x67 75 71 80 77 77 64 73

On push (dans le bon ordre svp ;-) et on place cette string encodée dans ebx:

push 0x77776473
push 0x67757180
mov ebx, esp    ' ebx contient maintenant notre clé "codée" 

Lorsque nous avons besoins de notre clé (au moment de la génération du KSA de notre RC4 par exemple), alors:

mov edx, 8              ' Nous avons 8 octets à décoder

decode:
  sub BYTE [ebx+edx], 0x3 ' on soustrait 3 
  dec edx
  jns decode

                        ' ebx contient donc maintenant notre clé en clair  

Il existe bien d’autres techniques pour masquer nos String d’une analyse statique de premier niveau. Nous en verrons d’autres dans la série de billets à venir sur les techniques ANTI- .

Une prochaine fois, nous analyserons un autre algorithme de chiffrement à clé symétrique en flux (Cipher Stream) très utilisé et proche des concepts de RC4 : SALSA20 …. Stay tuned